首先来举个栗子以便理解
比如说 集合A中所有的元素被分为1,2,3,4
那么集合A={1,2,3,4},各个元素都是独立的个体(如果学过编程语言的可能会更好理解)
集合的三大特性
1.确定性
可以用这么一个例子来概述:比如需要找出几个班级里高的男生,但是"高"这个概念是不确定的,所以我们不能将不确定的元素放入集合中,取而代之,我们可以使用一个确定的元素,比如"身高在180以上的男生",这是一个确定的数据,所以可以作为集合中的元素.这就是它的确定性。
2.互异性
互异性,顾名思义,就是一个集合之中的元素互不相同,比如A={1,1,2,3} B={1,2,3},那么A集合就是不存在且不成立的,言简意赅,一个集合中别有重复元素!
3.无序性
无序性,也是顾名思义,可以不按顺序来排列,比如A={1,3,2,4}和B={1,2,3,4}的意思都是相同的,很简单。
要注意的一点!
集合的命名必须是大写字母,比如A,B,C等;元素的命名需要使用小写字母,如a,b,c等

怎么表示从属关系呢?
比如集合A={1,2,3,4},则可以得出1∈{1,2,3,4}
(∈是属于的意思)
那不属于呢?
同理,如果114514不属于集合A,则可以表达为 114514∉{1,2,3,4}
(臭死了

关于实数集
实数集,也是顾名思义,集合里面都是实数便可以称为实数集,实数集在定义上即包含所有有理数和无理数的集合,现在学到的基本上都可以称为实数集(确信
关于虚数集这种东西现在就不解释了(主要是我也不懂,以后应该会学到
补充:实数集
实数集(R)可分为有理数集(Q)和无理数集,有理数集还可以分为整数集,如-2,-3,3......等等

集合的表示方法
1.列举法
例子:{1,2,3,4};{(1,2),(2,3)}
2.描述法
例子A={x|x<5,x∈R},那这个集合的意思就是包含小于五的所有数字,(x<5就是左边所满足的条件),那个x∈R是可加可不加的,意思是x属于实数辣
3.图像法
又称韦恩图法,是一种利用二维平面上的点集表示集合的方法。一般用平面上的矩形或圆形表示一个集合,是集合的一种直观的图形表示法[From百度知道]
例子如下图 A={1,2,3,4} B={3,4,5,6}
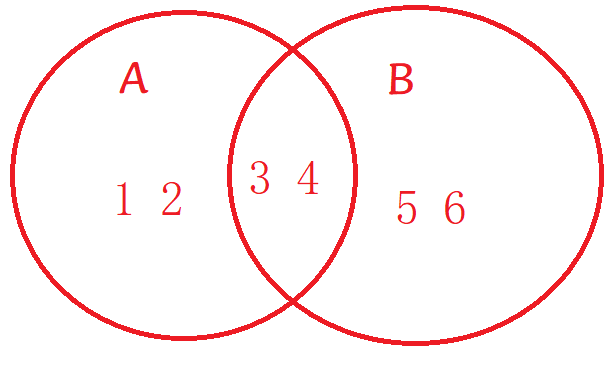
今天就到这里吧!bye!
明天可能有英语(

